I många utbildningar ingår problemlösning. Låt oss för enkelhetens skull kalla det för matematik, även om problemlösning finns inom nästan alla områden - fysik, kemi, biologi, ekonomi, läkemedelsberäkning, programmering ... you name it.
| Hos dem som har inkomsten 250 000 kronor går ungefär 20 procent av inkomsten till mat. De som tjänar mellan en halv och en miljon lägger bara 10 procent på mat. Och hos dem som tjänar över en miljon går bara 5 procent till mat. - Hur kan det komma sig att de som tjänar mest är minst hungriga? |
 |
Tre lektioner på universitetet
![]()
Under första lektionen fattar du 50 % och klagar tillsammans med dina kompisar över hur ostrukturerad läraren var.
Inför andra lektionen hoppas du på en förbättring men blir besviken. Lektionen byggde på den första och bara 25 % gick in i huvudet.
Efter tredje lektionen går du till studievägledaren för att byta program...
Ett bättre sätt
![]()
Före lektionerna tittar du igenom aktuellt material och försöker kanske också lösa några enkla uppgifter. Du är väl förberedd.
![]()
På lektionerna fattar du 75 %.
![]()
Efter lektionerna går du hem och "fattar resten". Du befäster det som sagts, och försöka reda ut det som var svårbegripligt.
Och det här är resultatet!
![]()
Hemligheten är alltså att läsa före och efter. Sammanfattningsvis kan man säga: Håll takten.
SÅ HÄR KAN DU LÖSA ETT PROBLEM
Här följer en mall för hur du kan ta dig an ett problem, till exempel en svår uppgift i matematik.
1. FÖRSÖK FÖRSTÅ PROBLEMET
Härma
Det mest grundläggande i all mänsklig inlärning är att härma. Glöm inte detta enormt viktiga ord - härma. Att ta efter, att imitera, att plagiera. I universitetsvärlden är plagiat närmast en svordom, men inte här och nu.
Ofta går läraren igenom tal på tavlan. Vi kan kalla dem typtal - typiska för det som ska läras. Vad gör sedan studenten? Jo, kastar sig entusiastiskt över boken och börjar räkna. Här är första felet. Du har låtit dig luras av att du förstått!
När läraren räknar på tavlan (och du förhoppningsvis samtidigt skriver i ditt block) får du en passiv förståelse. Du måste omvandla den till aktiv förståelse. Det gör du helt enkelt genom att räkna om typtalet. Först sedan går du till nästa nivå - den första egna uppgiften. Hoppa alltså inte till nästa nivå förrän du är mogen. Snart nog kommer du att få kasta dig över obekanta kluriga problem. |
För att bygga ett höghus måste man börja längst ner, och bygga sig uppåt. Våningarna vilar på varandra. Varje lektion i matte bygger på tidigare kunskaper. Är du en dag efter måste du se upp. Har du hamnat en vecka bakom kan du få stora problem. |
Visualisera och skriv fakta
Att visualisera problemet är att rita en bild över de samband som förekommer. Vilka fakta ges? Skriv upp alla relevanta data i figuren. Då får du en samlad bild över utgångspunkterna för att lösa problemet.
Här är en enkel uppgift för att visa tekniken:
| Familjen delade upp sin fjällresa i tre etapper. Första etappen körde de 38 % av den totala ressträckan och i den andra etappen 34 %. Hur långt åkte de i den tredje etappen, om de i den första åkte 19 mil? |
Den enkla visualiseringen kan se ut så här: 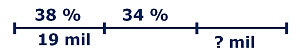
| Det är omöjligt att lära sig lösa problem endast genom att lyssna. Problemlösningens hela grej är att själv lösa problemen. Jämför med idrott; det är omöjligt att bli en hockeyspelare genom att titta eller lyssna på aldrig så många matcher. Man måste helt enkelt själv träna, träna och åter träna. |  |
 |
Matematik går inte att läsa fort. Varje ord, symbol och siffra är viktig och ofta måste man läsa rad för rad, siffra för siffra för att förstå. Snabbläsningsmetoder går alltså inte att använda. Ibland kan man tro att man läser väldigt långsamt då endast några sidor bearbetats under en hel dag, men tänk då på att en sida i matteboken inte alls går att jämföra med en sida i en ”läsebok”. |
Förenkla
Ibland kan det hjälpa att förenkla problemet. Du kan till exempel använda små heltal istället för höga decimaltal. Du kanske också kan formulera problemet i egna ord.
Skriv allt!
 När du löser ett problem, skriv då ut hela lösningskedjan som du skulle gjort på tentan. Rafsa inte ner endast några få rader för att sedan kolla i facit. Om du inte lär dig skriva ner hela lösningen kommer du att få problem på tentan, men än värre – när det blir svårare problem vet du inte hur du ska ställa upp dem. Och skriv tydligt! Oläsliga siffror och symboler är långt värre än oläsliga ord.
När du löser ett problem, skriv då ut hela lösningskedjan som du skulle gjort på tentan. Rafsa inte ner endast några få rader för att sedan kolla i facit. Om du inte lär dig skriva ner hela lösningen kommer du att få problem på tentan, men än värre – när det blir svårare problem vet du inte hur du ska ställa upp dem. Och skriv tydligt! Oläsliga siffror och symboler är långt värre än oläsliga ord.
Bryt ner i delproblem
Ett stort problem kan behöva brytas ner i mindre enheter, som först löses var för sig.
Ställ frågor tll dig själv
Ibland kan det vara bra att prata högt för sig själv. Om du tycker att gränsen till att vara tokig ligger farligt nära, kan du jobba tillsammans med en vän. Då slipper du prata med dig själv. |
|
Försök förstå vad det är som du inte förstår
Om du inte kommer vidare bör du utreda varför. Vad är det jag inte förstår? Är det själva problemet som jag inte kan greppa? Eller är det lösningsmetoden jag inte kommer på? Förstår jag inte orden och begreppen?
Fråga kompis – men kämpa först själv
 |
Så snart du har sett någon annans lösning av ett problem har du tappat en stor del av nyttan med problemlösning. Du tjänar oerhört mycket på att först försöka själv. Kämpa så mycket du bara kan innan du tittar på den lösning som någon annan tänkt ut. |
2. LÖS PROBLEMET
Ibland vet man inte riktigt vilken metod man ska använda, eller vilka formler som är relevanta. Kanske du till att börja med helt enkelt kan beskriva lösningen med ord, visualisera eller experimentera.
3. FÖRVANDLA TILL MATEMATIK
Om du använt en "hemmagjord" metod är det nu dags att förvandla dina resultat till matematiska formler och uppställningar.
4. SE TILLBAKA
- Är svaret jag fick rimligt?
- Använde jag en bra metod?
- Vad lärde jag mig för att i framtiden kunna lösa liknande problem?
![]()
![]()
Uppgift
Uppgiften är hämtad från en tenta i läkemedelsberäkning vid sjuksköterskeprogrammet på Mälardalens högskola.
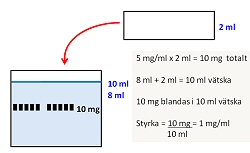
| En ampull innehåller 2 ml Apozepam med styrkan 5 mg/ml. Den ska spädas med 8 ml vatten. Vilken styrka får den spädda lösningen? |
Försök räkna ut själv innan du tittar på lösningsförslaget.
Förslag på lösning
Använd visualisering och skriv ner alla fakta.
Här har jag redan löst ett delproblem. Eftersom det är 2 ml vätska innehåller ampullen 10 mg Apozepam.

Häll lösningen i vattnet. Vattennivån höjs från 8 till 10 ml.
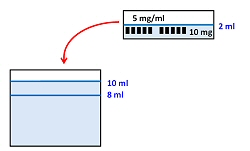
Även "substansen" hamnar i bägaren.
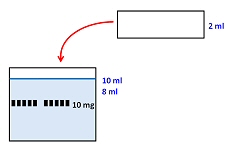
På mitt eget sätt räknar jag ut styrkan, som mäts i mg/ml (det ser jag i uppgiften)
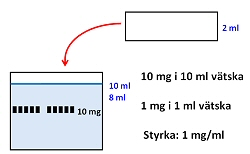
Jag förvandlar det jag gjort till en acceptabel formel som läraren kan acceptera.
Du har kommit till slutet av modul 8
PROBLEMLÖSNING
| Försök återge modulens huvudbudskap med hjälp av stödorden till vänster. |  |
 Du kanske behöver fråga dig saker som: Vad vet jag? Vad vet jag inte? Påminner det om något jag tidigare stött på? Finns det flera sätt att lösa problemet?
Du kanske behöver fråga dig saker som: Vad vet jag? Vad vet jag inte? Påminner det om något jag tidigare stött på? Finns det flera sätt att lösa problemet?